You might know that I love snapcubes. I think they are the most versatile type of thinking tool out there. I love how you aren't closed in to a single function, like many commercial manipulatives, and how tactile they are, how satisfying it is to snap them together and make something.They can be used in algebra, geometry, 2D and 3D measurement, playing with numbers, basically anything,
Cube tasks are their own genre of task, I think. There are lots just in the Ontario Spatial Reasoning monograph.
Here is a version of the 5 cube task you can use with most grades, with interesting results:
Here's the thing with that picture: cubes are something Minecraft does really well, seeing as how they are the basic unit in Minecraft (1 m^3, supposedly, in the actual game!)
So you might think, as per the SAMR model, that Minecraft is automatically better than using snapcubes. Isn't it fresher, newer, shinier, more "21st century"?
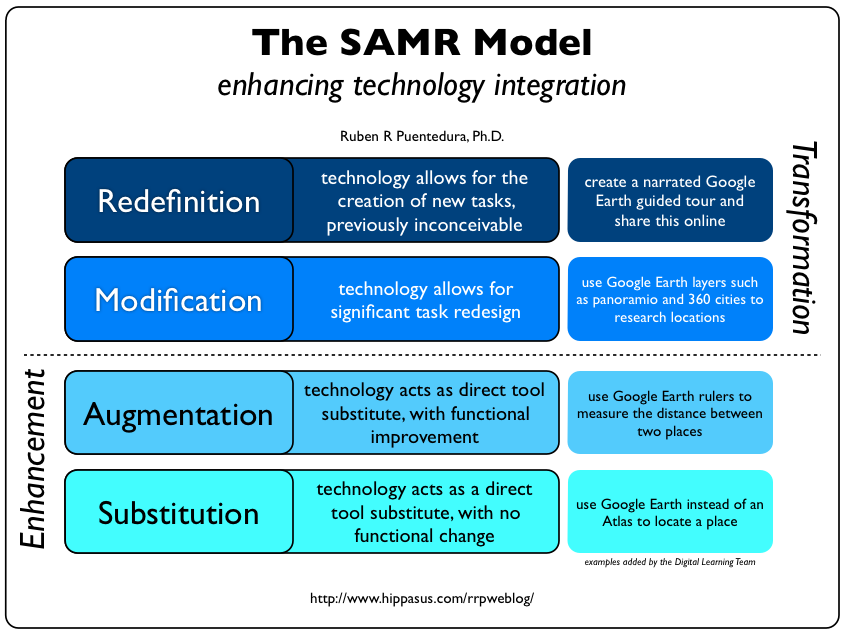
Not necessarily. Sometimes the original tools are better.
I came to @MrSoClassroom with this task in mind:
You have 24 cubes what is the least surface area? Greatest? @MatthewOldridge #engagemath
— Jonathan So (@MrSoclassroom) January 13, 2016
I thought, sure, we should offer Minecraft as an option, as well as snapcubes. I was persuaded otherwise? Why? One tool was enough, and it was the one built exactly for the job. Sometimes (actually, many times), physical manipulation is better than digital manipulation. Figuring out how to do the task in Minecraft (for non-players) would have slowed them down too much.
Further, one face of each cube placed on the ground would be hidden from view. That is a big problem with trying to do this task in Minecraft.
But you know what, about the Minecraft picture above? It just might be easier in Minecraft. Why? You will never run out of cubes, while trying to build your structures, in an infinite world...











